Pre-lecture materials

Read ahead

Before class, you can prepare by reading the following materials:

Prerequisites

Before starting you must install the additional package:

purrr - this provides a consistent functional programming interface to work with functions and vectors

You can do this by calling

install.packages("purrr")

Acknowledgements

Material for this lecture was borrowed and adopted from

Learning objectives

At the end of this lesson you will:

Be familiar with the concept of functional languages and functional styles of programming
Get comfortable with the major functions in purrr (e.g. the map family of functions)
Write your loops with map functions instead of the for loop

Motivation

If you have ever heard the phrase

“R is a functional language.”

you might have asked yourself what does this means exactly? Generally, this means that R lends itself nice to a particular style of programming, namely a functional style of programming (will explain more below), which is often very helpful to the types of problems you encounter when doing a data analysis.

Functional programming language

A functional style of programming is contrast to a the formal definition of a functional language (or functional programming, which can be complementary to object-oriented programming), which are languages that use functions to create conditional expressions to perform specific computations.

Differences between functional and object-oriented programming

From this resource some differences are:

Basic elements: The fundamental elements of object-oriented languages are objects and methods, while the elements of functional programming are functions and variables.
States: Object-oriented languages can change objects within the program, which means it has states or current modifications that affect the result of inputs. Functional languages do not use imperative programming, so they do not keep track of current states.
Parallel programming: This type of programming involves multiple computational processes occurring at the same time. Object-oriented languages have little support for parallel programming, but functional languages have extensive support for it.
Order: In object-oriented programming, computations occur in a specific order. In functional programming, computations can occur in any order.
Iterative data: Object-oriented programming uses loops, meaning repeated execution, for iterative data. Functional programming uses recursion for iterative data, meaning it attempts to solve problems using simpler versions of the same problem.

A traditional weakness of functional languages are poorer performance and sometimes unpredictable memory usage, but these have been much reduced in recent years.

Characteristics of a functional language

There are many definitions for precisely what makes a language functional, but there are two common threads and/or characteristics.

1. First-class functions

At it is core, functional programming treats functions equally as other data structures, called first class functions.

In R, this means that you can do many of the things with a function that you can do with a vector: you can assign them to variables, store them in lists, pass them as arguments to other functions, create them inside functions, and even return them as the result of a function.

Examples of cool things you can do with functions in R

Assign a function to a variable (foo):

foo <- function(){
  return("This is foo.")
}
class(foo)

[1] "function"

foo

function(){
  return("This is foo.")
}

foo()

[1] "This is foo."

You can store functions in a list:

foo_list <- list( 
  fun_1 = function() return("foo_1"),
  fun_2 = function() return("foo_2")
)

str(foo_list)

List of 2
 $ fun_1:function ()  
  ..- attr(*, "srcref")= 'srcref' int [1:8] 2 11 2 36 11 36 2 2
  .. ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x10c9994f8> 
 $ fun_2:function ()  
  ..- attr(*, "srcref")= 'srcref' int [1:8] 3 11 3 36 11 36 3 3
  .. ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x10c9994f8>

foo_list$fun_1()

[1] "foo_1"

foo_list$fun_2()

[1] "foo_2"

You can pass functions as arguments to other functions:

shell_fn <- function(f) f()
shell_fn(foo_list$fun_1)

[1] "foo_1"

shell_fn(foo_list$fun_2)

[1] "foo_2"

You can create functions inside of functions and return them as the result of a function

foo_wrap <- function(){
  foo_2 <- function(){
    return("This is foo_2.")
  }
  return(foo_2)
}

foo_wrap()

function(){
    return("This is foo_2.")
  }
<environment: 0x10d049120>

(foo_wrap())()

[1] "This is foo_2."

The bottom line, you can manipulate functions as the same way as you can to a vector or a matrix.

2. Pure functions

A function is pure, if it satisfies two properties:

The output only depends on the inputs, i.e. if you call it again with the same inputs, you get the same outputs. This excludes functions like runif(), read.csv(), or Sys.time() that can return different values.
The function has no side-effects, like changing the value of a global variable, writing to disk, or displaying to the screen. This excludes functions like print(), write.csv() and <-.

Pure functions are much easier to reason about, but obviously have significant downsides: imagine doing a data analysis where you could not generate random numbers or read files from disk.

Important

To be clear, R is not formally a functional programming language as it does not require pure functions to be used when writing code.

So you might be asking yourself, why are we talking about this then?

The formal definition of a functional programming language introduces a new style of programming, namely a functional style of programming.

Note

The key idea of a functional style is this programming style encourages programmers to write a big function as many smaller isolated functions, where each function addresses one specific task.

You can always adopt a functional style for certain parts of your code! For example, this style of writing code motivates more humanly readable code, and recyclable code.

"data_set.csv" |> 
  import_data_from_file() |> 
  data_cleaning() |> 
  run_regression() |>
  model_diagnostics() |>
  model_visualization()

"data_set2.csv" |> 
  import_data_from_file() |> 
  data_cleaning() |> 
  run_different_regression() |>
  model_diagnostics() |>
  model_visualization()

Functional style

At a high-level, a functional style is the concept of decomposing a big problem into smaller components, then solving each piece with a function or combination of functions.

When using a functional style, you strive to decompose components of the problem into isolated functions that operate independently.
Each function taken by itself is simple and straightforward to understand; complexity is handled by composing functions in various ways.

Functionals

In this lecture, we will focus on one type of functional technique, namely functionals, which are functions that take another function as an argument and returns a vector as output.

Functionals allow you to take a function that solves the problem for a single input and generalize it to handle any number of inputs. Once you learn about them, you will find yourself using them all the time in data analysis.

Example of a functional

Here’s a simple functional: it calls the function provided as input with 1000 random uniform numbers.

randomise <- function(f) f(runif(1e3))
randomise(mean)

[1] 0.5055154

randomise(mean)

[1] 0.5032077

randomise(sum)

[1] 507.0181

The chances are that you have already used a functional. You might have used for-loop replacements like base R’s lapply(), apply(), and tapply() or maybe you have used a mathematical functional like integrate() or optim().

One of the most common use of functionals is an alternative to for loops.

For loops have a bad rap in R because many people believe they are slow, but the real downside of for loops is that they’re very flexible: a loop conveys that you’re iterating, but not what should be done with the results.

Typically it is not the for loop itself that is slow, but what you are doing inside of it. A common culprit of slow loops is modifying a data structure, where each modification generates a copy.

If you’re an experienced for loop user, switching to functionals is typically a pattern matching exercise. You look at the for loop and find a functional that matches the basic form. If one does not exist, do not try and torture an existing functional to fit the form you need. Instead, just leave it as a for loop! (Or once you have repeated the same loop two or more times, maybe think about writing your own functional).

Just as it is better to use while than repeat, and it’s better to use for than while, it is better to use a functional than for.

Each functional is tailored for a specific task, so when you recognize the functional you immediately know why it’s being used.

`purrr`: the functional programming toolkit

The R package purrr as one important component of the tidyverse, provides a interface to manipulate vectors in the functional style.

purrr enhances R’s functional programming (FP) toolkit by providing a complete and consistent set of tools for working with functions and vectors.

purrr cheatsheet

It is very difficult, if not impossible, to remember all functions that a package offers as well as their use cases.

Hence, purrr developers offer a nice compact cheatsheet with visualizations at https://github.com/rstudio/cheatsheets/blob/main/purrr.pdf.

Similar cheat sheets are available for other tidyverse packages.

The most popular function in purrr is map() which iterates over the supplied data structure and apply a function during the iterations. Beside the map() function,purrr also offers a series of useful functions to manipulate the list data frame.

The `map` family

The most fundamental functional in the purrr package is the map(.x, .f) function. It takes a vector (.x) and a function (.f), calls the function once for each element of the vector, and returns the results in a list. In other words, map(1:3, f) is equivalent to list(f(1), f(2), f(3)).

library(purrr)

# we create a function called "triple"
triple <- function(x) x * 3

# using for loop to iterate over a vector
loop_ret <- list()
for(i in 1:3){
  loop_ret[i] <- triple(i)
}
loop_ret

[[1]]
[1] 3

[[2]]
[1] 6

[[3]]
[1] 9

# map implementation to iterate over a vector
map_eg1 <- map(.x = 1:3, .f = triple)
map_eg2 <- map(.x = 1:3, .f = function(x) triple(x)) # create an inline anonymous function
map_eg3 <- map(.x = 1:3, .f = ~triple(.x)) # same as above, but special purrr syntax with a "twiddle"


identical(loop_ret,map_eg1)

[1] TRUE

identical(loop_ret,map_eg2)

[1] TRUE

identical(loop_ret,map_eg3)

[1] TRUE

Or, graphically this is what map() is doing:

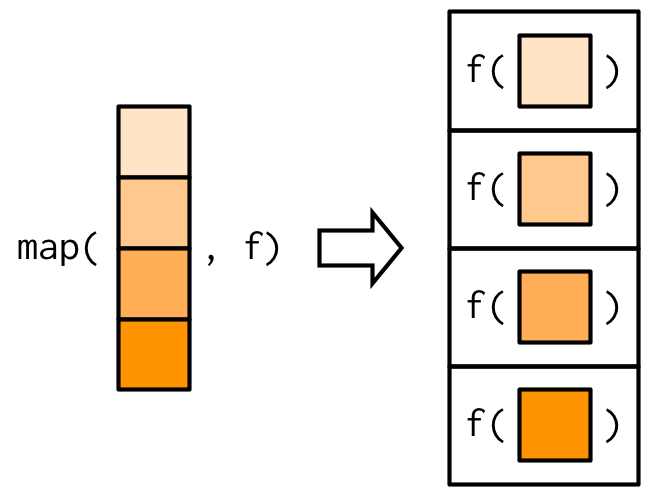
How does map relate to functional programming in base R?

map() returns a list, which makes it the most general of the map family because you can put anything in a list.

The base equivalent to map(.x, .f) is lapply(X, FUN).

Because the arguments include functions (.f) besides data (.x), map() functions are considered as a convenient interface to implement functional programming.

`map` variants

Sometimes it is inconvenient to return a list when a simpler data structure would do, so there are four more specific variants of map that make it really a family of functions (of syntax map_*()).

map_lgl()
map_int()
map_dbl()
map_chr()

For example, purrr uses the convention that suffixes, like _dbl(), refer to the output. Each returns an atomic vector of the specified type:

# map_chr() always returns a character vector
map_chr(.x = mtcars, .f = typeof)

     mpg      cyl     disp       hp     drat       wt     qsec       vs 
"double" "double" "double" "double" "double" "double" "double" "double" 
      am     gear     carb 
"double" "double" "double"

# map_lgl() always returns a logical vector
map_lgl(.x = mtcars, .f = is.double)

 mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE TRUE

# map_int() always returns a integer vector
n_unique <- function(x) length(unique(x))
map_int(.x = mtcars, .f = n_unique)

 mpg  cyl disp   hp drat   wt qsec   vs   am gear carb 
  25    3   27   22   22   29   30    2    2    3    6

# map_dbl() always returns a double vector
map_dbl(.x = mtcars, .f = mean)

       mpg        cyl       disp         hp       drat         wt       qsec 
 20.090625   6.187500 230.721875 146.687500   3.596563   3.217250  17.848750 
        vs         am       gear       carb 
  0.437500   0.406250   3.687500   2.812500

Pro-tip

All map_*() functions can take any type of vector as input. The examples above rely on two facts:

mtcars is a data.frame. In R, data.frame is a special case of list, where each column as one item of the list. Don’t confuse with each row as an item.

class(mtcars)

[1] "data.frame"

typeof(mtcars)

[1] "list"

All map functions always return an output vector the same length as the input, which implies that each call to .f must return a single value. If it does not, you will get an error:

pair <- function(x) c(x, x)
map_dbl(.x = 1:2, .f = pair)

Error in `map_dbl()`:
ℹ In index: 1.
Caused by error:
! Result must be length 1, not 2.

This is similar to the error you will get if .f returns the wrong type of result:

map_dbl(1:2, as.character)

Error in `map_dbl()`:
ℹ In index: 1.
Caused by error:
! Can't coerce from a string to a double.

Question

Let’s assume I have a dataframe called tmp_dat. How would I use map() to calculate the mean for the columns?

tmp_dat <- data.frame(
  x = 1:5,
  y = 6:10
)

## try it out

Question

Can we re-write the map() function above to use tmp_data as input with the |> operator?

## try it out

Passing arguments with `...`

It is often convenient to pass along additional arguments to the function that you are calling.

For example, you might want to pass na.rm = TRUE along to mean(). One way to do that is with an anonymous function:

x <- list(1:5, c(1:10, NA))
map_dbl(x, ~ mean(.x, na.rm = TRUE))

[1] 3.0 5.5

But because the map functions pass ... along, there is a simpler form available:

map_dbl(x, mean, na.rm = TRUE)

[1] 3.0 5.5

This is easiest to understand with a picture: any arguments that come after f in the call to map() are inserted after the data in individual calls to f():

Note

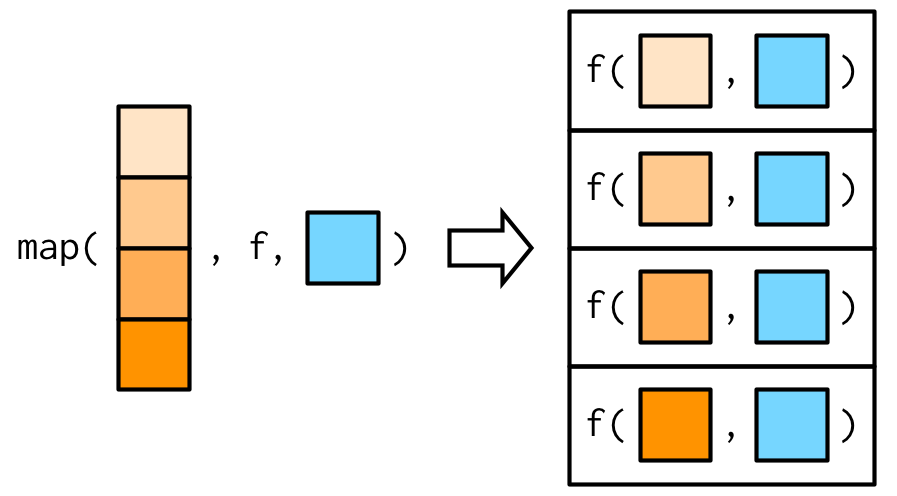
It’s important to note that these arguments are not decomposed; or said another way, map() is only vectorised over its first argument.

If an argument after f is a vector, it will be passed along as is:

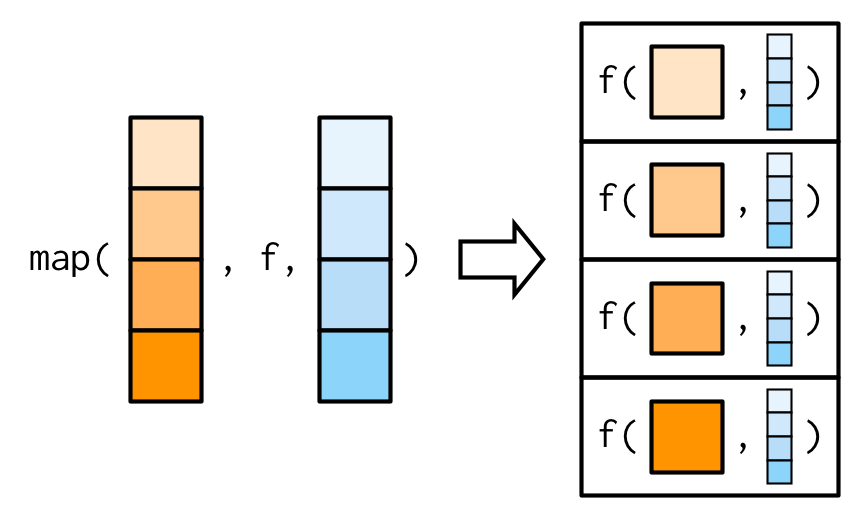
Stratified analysis with `map`

Before we go on to explore more map variants, let’s take a quick look at how you tend to use multiple purrr functions to solve a moderately realistic problem: fitting a model to each subgroup and extracting a coefficient of the model.

For this toy example, I will break the mtcars data set down into groups defined by the number of cylinders, using the base split function:

# different numbers of cylinders
unique(mtcars$cyl)

[1] 6 4 8

by_cyl <- split(mtcars, mtcars$cyl)
length(by_cyl)

[1] 3

str(by_cyl)

List of 3
 $ 4:'data.frame':  11 obs. of  11 variables:
  ..$ mpg : num [1:11] 22.8 24.4 22.8 32.4 30.4 33.9 21.5 27.3 26 30.4 ...
  ..$ cyl : num [1:11] 4 4 4 4 4 4 4 4 4 4 ...
  ..$ disp: num [1:11] 108 146.7 140.8 78.7 75.7 ...
  ..$ hp  : num [1:11] 93 62 95 66 52 65 97 66 91 113 ...
  ..$ drat: num [1:11] 3.85 3.69 3.92 4.08 4.93 4.22 3.7 4.08 4.43 3.77 ...
  ..$ wt  : num [1:11] 2.32 3.19 3.15 2.2 1.61 ...
  ..$ qsec: num [1:11] 18.6 20 22.9 19.5 18.5 ...
  ..$ vs  : num [1:11] 1 1 1 1 1 1 1 1 0 1 ...
  ..$ am  : num [1:11] 1 0 0 1 1 1 0 1 1 1 ...
  ..$ gear: num [1:11] 4 4 4 4 4 4 3 4 5 5 ...
  ..$ carb: num [1:11] 1 2 2 1 2 1 1 1 2 2 ...
 $ 6:'data.frame':  7 obs. of  11 variables:
  ..$ mpg : num [1:7] 21 21 21.4 18.1 19.2 17.8 19.7
  ..$ cyl : num [1:7] 6 6 6 6 6 6 6
  ..$ disp: num [1:7] 160 160 258 225 168 ...
  ..$ hp  : num [1:7] 110 110 110 105 123 123 175
  ..$ drat: num [1:7] 3.9 3.9 3.08 2.76 3.92 3.92 3.62
  ..$ wt  : num [1:7] 2.62 2.88 3.21 3.46 3.44 ...
  ..$ qsec: num [1:7] 16.5 17 19.4 20.2 18.3 ...
  ..$ vs  : num [1:7] 0 0 1 1 1 1 0
  ..$ am  : num [1:7] 1 1 0 0 0 0 1
  ..$ gear: num [1:7] 4 4 3 3 4 4 5
  ..$ carb: num [1:7] 4 4 1 1 4 4 6
 $ 8:'data.frame':  14 obs. of  11 variables:
  ..$ mpg : num [1:14] 18.7 14.3 16.4 17.3 15.2 10.4 10.4 14.7 15.5 15.2 ...
  ..$ cyl : num [1:14] 8 8 8 8 8 8 8 8 8 8 ...
  ..$ disp: num [1:14] 360 360 276 276 276 ...
  ..$ hp  : num [1:14] 175 245 180 180 180 205 215 230 150 150 ...
  ..$ drat: num [1:14] 3.15 3.21 3.07 3.07 3.07 2.93 3 3.23 2.76 3.15 ...
  ..$ wt  : num [1:14] 3.44 3.57 4.07 3.73 3.78 ...
  ..$ qsec: num [1:14] 17 15.8 17.4 17.6 18 ...
  ..$ vs  : num [1:14] 0 0 0 0 0 0 0 0 0 0 ...
  ..$ am  : num [1:14] 0 0 0 0 0 0 0 0 0 0 ...
  ..$ gear: num [1:14] 3 3 3 3 3 3 3 3 3 3 ...
  ..$ carb: num [1:14] 2 4 3 3 3 4 4 4 2 2 ...

This creates a list of three data frames: the cars with 4, 6, and 8 cylinders respectively.

First, imagine we want to fit a linear model to understand how the miles per gallon (mpg) associated with the weight (wt). We can do this for all observations in mtcars using:

lm(mpg ~ wt, data = mtcars)


Call:
lm(formula = mpg ~ wt, data = mtcars)

Coefficients:
(Intercept)           wt  
     37.285       -5.344

The following code shows how you might do that with purrr, which returns a list with output from each lm fit for each cylinder:

by_cyl |>
  map(.f = ~ lm(mpg ~ wt, data = .x))

$`4`

Call:
lm(formula = mpg ~ wt, data = .x)

Coefficients:
(Intercept)           wt  
     39.571       -5.647  


$`6`

Call:
lm(formula = mpg ~ wt, data = .x)

Coefficients:
(Intercept)           wt  
      28.41        -2.78  


$`8`

Call:
lm(formula = mpg ~ wt, data = .x)

Coefficients:
(Intercept)           wt  
     23.868       -2.192

Question

Let’s say we wanted to extract the second coefficient (i.e. the slope). Using all the observations in mtcars (i.e. ignoring cyl), it would be something like this:

lm.fit <- lm(mpg ~ wt, data = mtcars)
coef(lm.fit)

(Intercept)          wt 
  37.285126   -5.344472

coef(lm.fit)[2]

       wt 
-5.344472

How would we do this with the map() family functions if we wanted to stratify the analysis for each cyl?

Hint: you can use two map functions (e.g. map() and map_dbl(2) where you can extract a specific element by a specific name or position).

## try it out

Or, of course, you could use a for loop:

slopes <- double(length(by_cyl))
for (i in seq_along(by_cyl)) {
  model <- lm(mpg ~ wt, data = by_cyl[[i]])
  slopes[[i]] <- coef(model)[[2]]
}
slopes

[1] -5.647025 -2.780106 -2.192438

It’s interesting to note that as you move from purrr to base apply functions to for loops you tend to do more and more in each iteration.

In purrr we iterate 3 times (map(), map(), map_dbl()), and with a for loop we iterate once. I prefer more, but simpler, steps because I think it makes the code easier to understand and later modify.

Question

Now we are interested in calculating the average mpg for vehicles with different numbers of cylinders. How can we use map functions to do this? You can return a list.

Hint: You can use the syntax x$mpg where x is a dataframe within a map function.

## try it out

Matrix as the output

The map family include functions that organize the output in different data structures, whose names follow the pattern map_*. As we’ve seen, the map function return a list. The following functions will return a vector of a specific kind, e.g. map_lgl returns a vector of logical variables, map_chr returns a vector of strings.

It is also possible to return the the results as data frames by

row binding (map_dfr) or
column binding (map_dfc)

by_cyl |> 
  map_dbl(.f = ~mean(.x$mpg)) # returns a vector of doubles

       4        6        8 
26.66364 19.74286 15.10000

by_cyl |> 
  map_dfr(.f = ~colMeans(.x)) # return a data frame by row binding

# A tibble: 3 × 11
    mpg   cyl  disp    hp  drat    wt  qsec    vs    am  gear  carb
  <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1  26.7     4  105.  82.6  4.07  2.29  19.1 0.909 0.727  4.09  1.55
2  19.7     6  183. 122.   3.59  3.12  18.0 0.571 0.429  3.86  3.43
3  15.1     8  353. 209.   3.23  4.00  16.8 0     0.143  3.29  3.5

by_cyl |> 
  map_dfc(.f = ~colMeans(.x)) # return a data frame by col binding

# A tibble: 11 × 3
       `4`     `6`     `8`
     <dbl>   <dbl>   <dbl>
 1  26.7    19.7    15.1  
 2   4       6       8    
 3 105.    183.    353.   
 4  82.6   122.    209.   
 5   4.07    3.59    3.23 
 6   2.29    3.12    4.00 
 7  19.1    18.0    16.8  
 8   0.909   0.571   0    
 9   0.727   0.429   0.143
10   4.09    3.86    3.29 
11   1.55    3.43    3.5

More map variants

There are 23 primary variants of map(). So far, we have learned about five (map(), map_lgl(), map_int(), map_dbl() and map_chr()). That means that you have got 18 (!!) more to learn. That sounds like a lot, but fortunately the design of purrr means that you only need to learn five new ideas:

Output same type as input with modify()
Iterate over two inputs with map2().
Iterate with an index using imap()
Return nothing with walk().
Iterate over any number of inputs with pmap().

The map family of functions has orthogonal input and outputs, meaning that we can organise all the family into a matrix, with inputs in the rows and outputs in the columns. Once you have mastered the idea in a row, you can combine it with any column; once you have mastered the idea in a column, you can combine it with any row. That relationship is summarised in the following table:

	List	Atomic	Same type	Nothing
One argument	`map()`	`map_lgl()`, …	`modify()`	`walk()`
Two arguments	`map2()`	`map2_lgl()`, …	`modify2()`	`walk2()`
One argument + index	`imap()`	`imap_lgl()`, …	`imodify()`	`iwalk()`
N arguments	`pmap()`	`pmap_lgl()`, …	—	`pwalk()`

`modify()`

Imagine you wanted to double every column in a data frame. You might first try using map(), but map() always returns a list:

df <- data.frame(
  x = 1:3,
  y = 6:4
)

map(df, ~ .x * 2)

$x
[1] 2 4 6

$y
[1] 12 10  8

If you want to keep the output as a data frame, you can use modify(), which always returns the same type of output as the input:

modify(df, ~ .x * 2)

Note

Despite the name, modify() doesn’t modify in place, it returns a modified copy, so if you wanted to permanently modify df, you’d need to assign it:

df <- modify(df, ~ .x * 2)

`map2()` and friends

map() is vectorised over a single argument, .x.

This means it only varies .x when calling .f, and all other arguments are passed along unchanged, thus making it poorly suited for some problems.

For example, how would you find a weighted mean when you have a list of observations and a list of weights? Imagine we have the following data:

xs <- map(1:8, ~ runif(10))
xs[[1]][[1]] <- NA
ws <- map(1:8, ~ rpois(10, 5) + 1)

You can use map_dbl() to compute the unweighted means:

map_dbl(.x = xs, .f = mean)

[1]        NA 0.6596358 0.6001102 0.3955773 0.4220107 0.6470785 0.2633766
[8] 0.6809399

But passing ws as an additional argument does not work because arguments after .f are not transformed:

map_dbl(x. = xs, .f = weighted.mean, w = ws)

Error in map_dbl(x. = xs, .f = weighted.mean, w = ws): argument ".x" is missing, with no default

We need a new tool: a map2(), which is vectorised over two arguments. This means both .x and .y are varied in each call to .f:

map2_dbl(.x = xs, .y = ws, .f = weighted.mean)

[1]        NA 0.6461823 0.5858559 0.3832126 0.4033124 0.6399419 0.2586362
[8] 0.6835747

The arguments to map2() are slightly different to the arguments to map() as two vectors come before the function, rather than one. Additional arguments still go afterwards:

map2_dbl(.x = xs, .y = ws, .f = weighted.mean, na.rm = TRUE)

[1] 0.5480634 0.6461823 0.5858559 0.3832126 0.4033124 0.6399419 0.2586362
[8] 0.6835747

`walk()` and friends

Most functions are called for the value that they return, so it makes sense to capture and store the value with a map() function.

But some functions are called primarily for their side-effects (e.g. cat(), write.csv(), or ggsave()) and it does not make sense to capture their results.

Let’s consider the example of saving a dataset. In this case, map will force an output, e.g. NULL. One can consider using walk instead. The function walk (and walk2 for more than two inputs) behaves exactly the same as map but does not output anything.

tmp_fldr <- tempdir()

map2(.x = by_cyl,
     .y = 1:length(by_cyl),
     .f = ~saveRDS(.x, 
                   file = paste0(tmp_fldr, "/",.y, ".rds"))
)

$`4`
NULL

$`6`
NULL

$`8`
NULL

# No output
walk2(.x = by_cyl,
      .y = (1:length(by_cyl)),
      .f = ~saveRDS(.x, 
                    file = paste0(tmp_fldr, "/",.y, ".rds"))
)

Summary

Introduction to functional programming.
The R package purrr provides a nice interface to functional programming and list manipulation.
The function map and its aternative map_* provide a neat way to iterate over a list or vector with the output in different data structures.
The function map2 and pmap allow having more than one list as input.
The function walk and its alternatives walk2, walk_*, which do not provide any output.

Post-lecture materials

Questions

Use as_mapper() to explore how purrr generates anonymous functions for the integer, character, and list helpers. What helper allows you to extract attributes? Read the documentation to find out.
map(1:3, ~ runif(2)) is a useful pattern for generating random numbers, but map(1:3, runif(2)) is not. Why not? Can you explain why it returns the result that it does?
Can you write a section of code to demonstrate the central limit theorem primarily using the purrr package and/or using the R base package?
Use the appropriate map() function to:
1. Compute the standard deviation of every column in a numeric data frame.
2. Compute the standard deviation of every numeric column in a mixed data frame. (Hint: you will need to do it in two steps.)
3. Compute the number of levels for every factor in a data frame.
The following code simulates the performance of a t-test for non-normal data. Extract the p-value from each test, then visualise.
```
trials <- map(1:100, ~ t.test(rpois(10, 10), rpois(7, 10)))
```

Use map() to fit linear models to the mtcars dataset using the formulas stored in this list:

formulas <- list(
  mpg ~ disp,
  mpg ~ I(1 / disp),
  mpg ~ disp + wt,
  mpg ~ I(1 / disp) + wt
)

Fit the model mpg ~ disp to each of the bootstrap replicates of mtcars in the list below, then extract the $R^2$ of the model fit (Hint: you can compute the $R^2$ with summary().)
```
bootstrap <- function(df) {
  df[sample(nrow(df), replace = TRUE), , drop = FALSE]
}

bootstraps <- map(1:10, ~ bootstrap(mtcars))
```

Additional Resources

Tip

Pre-lecture materials

Read ahead

Prerequisites

Acknowledgements

Learning objectives

Motivation

Functional programming language

Characteristics of a functional language

1. First-class functions

2. Pure functions

Functional style

Functionals

purrr: the functional programming toolkit

The map family

map variants

Passing arguments with ...

Stratified analysis with map

Matrix as the output

More map variants

modify()

map2() and friends

walk() and friends

Summary

Post-lecture materials

Additional Resources

`purrr`: the functional programming toolkit

The `map` family

`map` variants

Passing arguments with `...`

Stratified analysis with `map`

`modify()`

`map2()` and friends

`walk()` and friends